Construção Geométrica da Parábola pelo Método de Werner

No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque neesa época.

Werner produziu uma obra importante para a Geometria sobre Elementos de Cônicas, em latim, dividida em $22$ volumes, impressa em Nüremberg em $1522$.

Werner estava preocupado com o problema da duplicação do cubo e, então, concentrou-se muito com curvas como a parábola e a hipérbole. Ele dá uma construção interessante, utilizando apenas régua e compasso:

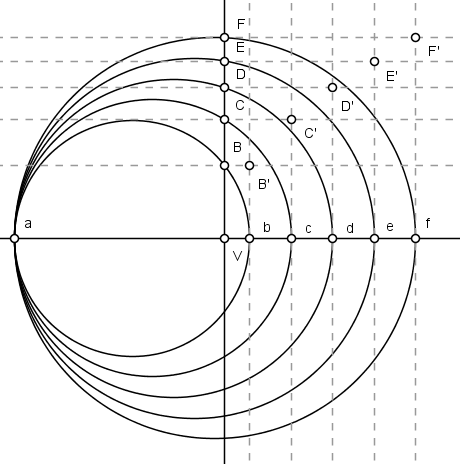
$1)$ Num eixo horizontal, descrevemos um feixe de circunferências tangentes entre si no ponto $a$, cortando o eixo normal nos pontos $b$, $c$, $d$, $e$, $f$, $\cdots$, de modo que as distâncias $\overline{bc}=\overline{cd}=\overline{de}=\cdots$.

$2)$ Marcamos uma distância $\overline{aV}$ igual a um parâmetro desejado sobre a normal e por $V$ traçamos uma perpendicular, cortando as circunferências nos pontos $B$, $C$, $D$, $E$, $F$, $\cdots$, respectivamente.

$3)$ Por $b$, traçamos os segmentos $\overline{bB'}$ e $\overline{bB''}$, perpendiculares à normal e de comprimento igual à $\overline{VB}$. Obtemos facilmente traçando paralelas à normal no ponto $B$. Por $c$, traçamos os segmentos $\overline{cC'}$ e $\overline{cC''}$, perpendiculares à normal e de comprimento igual à $\overline{VC}$. Procedemos analogamente para os pontos $d$, $e$, $f$, $\cdots$

$4)$ Os pontos $B'$, $B''$, $C'$, $C''$, $D'$, $D''$, $\cdots$ estão sobre a parábola de vértice $V$, cujo eixo de simetria é a normal.

Referências:

[1] História da Matemática - Carl Boyer