Este artigo é melhor visualizado em computadores, devido às fórmulas longas. Se estiver acessando pelo celular, ative o modo "para computador".
Veremos neste artigo como calcular as medidas dos ângulos internos de um triângulo qualquer em função de seus lados através de fórmulas de radicais aninhados.
Dado um triângulo $\triangle ABC$, de lados $a$, $b$, $c$. Os ângulos internos $\alpha$, $\beta$ e $\gamma$ podem ser calculados com ótima aproximação através das fórmulas:
$$\alpha \approx \frac{180 \cdot 2^5}{\pi} \ \sqrt{2- \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}} \tag{1}
$$
$$
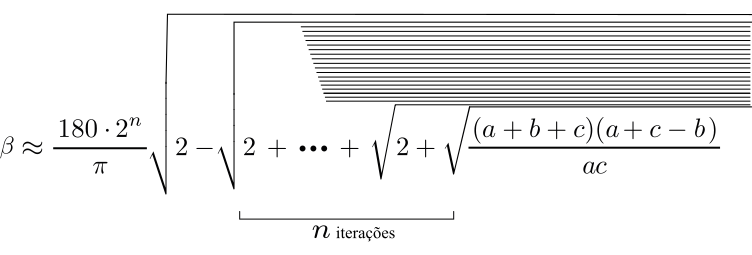
\beta \approx \frac{180 \cdot 2^5}{\pi} \ \sqrt{2- \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{\frac{(a+b+c)(a+c-b)}{ac}}}}}}} \tag{2}
$$
$$
\gamma \approx \frac{180 \cdot 2^5}{\pi} \ \sqrt{2- \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{\frac{(a+b+c)(a+b-c)}{ab}}}}}}} \tag{3}
$$
Demonstração
O método consiste em criar uma circunferência centrada em um dos vértices do triângulo $\triangle ABC$ com raio igual a um dos lados adjacentes ao ângulo. Na figura abaixo, o centro está localizado no vértice $A$ e o raio da circunferência é igual ao lado $b$.
[Figura 2: ângulos de um triângulo]
Aplicando a Lei dos Cossenos no triângulo $\triangle ABC$, o $\cos (\alpha)$, em função dos lados $a$, $b$ e $c$, é dado por:
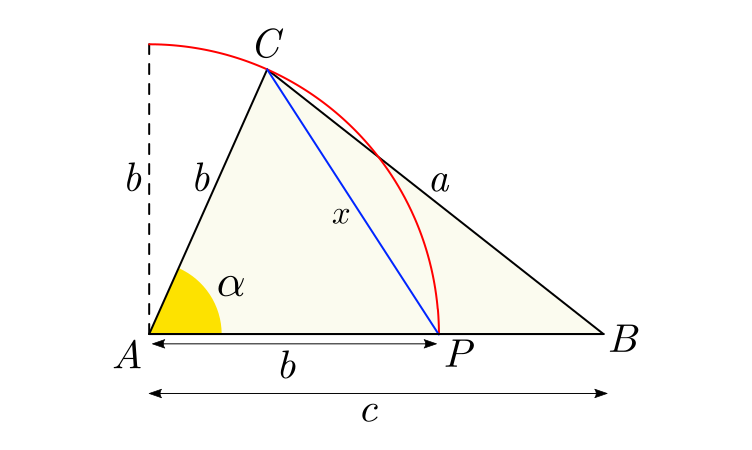
$$\cos(\alpha) = \frac{b^2+c^2-a^2}{2bc} \tag{4}
$$
Se o comprimento do arco $\widehat{CP}$ for conhecido, poderemos encontrar $\alpha$ em graus utilizando a seguinte proporção: O produto do raio $b$ por $\pi$ está para $180^\circ$, assim como o arco $\widehat{CP}$ está para o ângulo $\alpha$:
\frac{\pi b}{180^\circ} = \frac{\widehat{CP}}{\alpha} \tag{5}
$$
Traçando um segmento de reta que inicia-se no vértice $C$ e prolonga-se até o ponto $P$, como mostrado na figura abaixo:
[Figura 3: Ângulos de um triângulo]
No triângulo $\triangle ACP$, o comprimento $x$ pode ser obtido pela Lei dos Cossenos, sendo assim, podemos substituir $\widehat{CP}$ por $x$ na relação $(5)$. Portanto, agora somos capazes de calcular a medida de $\alpha$, embora seja uma aproximação ruim, uma vez que o arco $\widehat{CP}>x$:
$$\frac{\pi b}{180^\circ} = \frac{x}{\alpha} \tag{6}
$$
Isolando o ângulo $\alpha$:
$$\alpha = \frac{180^\circ \cdot x}{\pi b} \tag{7}
$$
A segunda parte do método consiste em reduzir o segmento $x$ até coincidir com uma pequena parte do arco $\widehat{CP}$. Desse modo, obteremos $\alpha$ com uma boa precisão. No entanto, para que o método funcione é necessário que o novo ângulo tenha relação direta com $\alpha$. Há uma identidade trigonométrica que relaciona o ângulo com a sua metade, conhecida como a fórmula do cosseno do arco metade, assim, poderemos reduzir o comprimento de $x$ ao mesmo tempo que dividimos ao meio o ângulo $\alpha$:
[Figura 4: 1ª iteração]
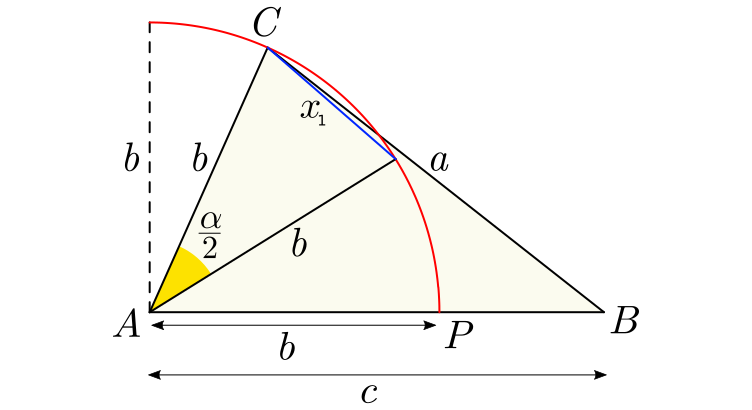
\cos \left( \frac{\alpha}{2} \right) = \pm \sqrt{\frac{1+\cos (\alpha)}{2}} \tag{8}
$$
A relação $(8)$ fornece duas opções:
$$
\cos \left( \frac{\alpha}{2} \right) = \sqrt{\frac{1+\cos (\alpha)}{2}} \tag{9}
$$
$$
\cos \left( \frac{\alpha}{2} \right) = - \sqrt{\frac{1+\cos (\alpha)}{2}} \tag{10}
$$
A relação $(10)$ não utilizaremos. Por que? A divisão ao meio de qualquer ângulo de um triângulo está limitado ao primeiro quadrante, de modo que $\displaystyle 0< \frac{\alpha}{2} < 90^{\circ}$, portanto, temos que $\displaystyle \cos \left( \frac{\alpha}{2}\right) > 0$. Como conhecemos o cosseno de $\alpha$ pela relação $(4)$, poderemos substituí-lo em $(9)$:
$$\cos \left(\frac{\alpha}{2}\right) = \sqrt{\frac{1+\displaystyle \left( \frac{b^2+c^2-a^2}{2bc} \right)}{2}} \tag{11}
$$
Simplificando o radicando:
$$\cos \left(\frac{\alpha}{2}\right) = \sqrt{ \frac{2bc+b^2+c^2-a^2}{4bc} }\tag{12}
$$
$$
\cos \left(\frac{\alpha}{2}\right) = \sqrt{\frac{(b+c)^2-a^2}{4bc}} \tag{13}
$$
$$
\cos \left(\frac{\alpha}{2}\right) = \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}} \tag{14}
$$
Dividindo o ângulo $\displaystyle \frac{\alpha}{2}$ ao meio, obtemos:
[Figura 5: 2ª iteração]
\cos \left(\frac{\alpha}{4}\right) = \sqrt{\frac{\displaystyle 1+\cos \left(\frac{\alpha}{2}\right)}{2}} \tag{15}
$$
Substituindo $(14)$ em $(15)$, obtemos:
$$\cos \left(\frac{\alpha}{4}\right) = \sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}} \tag{16}
$$
Dividindo o ângulo $\displaystyle \frac{\alpha}{4}$ ao meio:
[Figura 6: 3ª iteração]
$$
\cos \left(\frac{\alpha}{8}\right) = \sqrt{\frac{\displaystyle 1+\cos \left(\frac{\alpha}{4}\right)}{2}} \tag{17}
$$
\cos \left(\frac{\alpha}{8}\right) = \sqrt{\frac{\displaystyle 1+\cos \left(\frac{\alpha}{4}\right)}{2}} \tag{17}
$$
Substituindo $(16)$ em $(17)$, obtemos:
$$\cos \left(\frac{\alpha}{8}\right) = \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}} \tag{18}
$$
Dividindo o ângulo $\displaystyle \frac{\alpha}{8}$ ao meio:
[Figura 7: 4ª iteração]
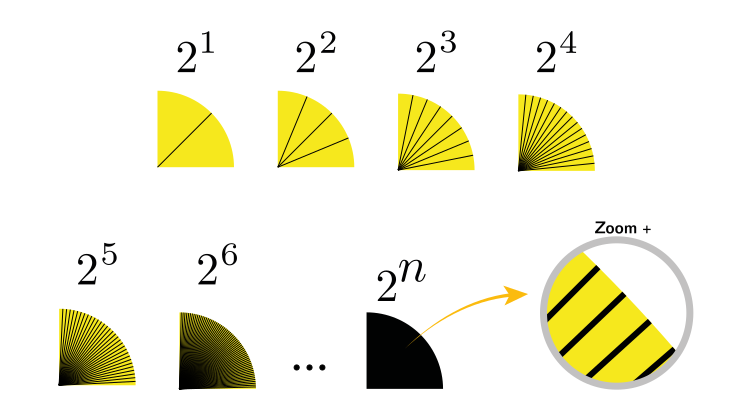
\cos \left(\frac{\alpha}{16}\right) = \sqrt{\frac{\displaystyle 1+\cos \left(\frac{\alpha}{8}\right)}{2}} \tag{19}
$$
Substituindo $(18)$ em $(19)$, obtemos:
$$\cos \left(\frac{\alpha}{16}\right) = \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}} \tag{20}
$$
Dividindo o ângulo $\displaystyle \frac{\alpha}{16}$ o meio:
[Figura 8: 5º iteração]
Com $5$ iterações, o comprimento de $x_5 \approx \widehat{CQ}$. Vamos parar por aqui:
$$\cos \left(\frac{\alpha}{32}\right) = \sqrt{\frac{\displaystyle 1+\cos \left(\frac{\alpha}{16}\right)}{2}} \tag{21}
$$
Substituindo $(20)$ em $(21)$, obtemos:
$$\cos \left(\frac{\alpha}{32}\right) = \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}} \tag{22}
$$
Pela lei dos cossenos, o comprimento de $x_5$ é igual a:
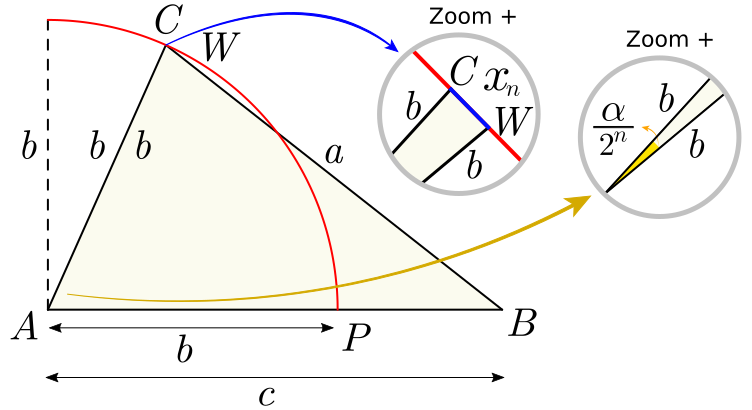
$$x_5^2 = b^2+b^2-2\cdot b \cdot b \cdot \cos\left(\frac{\alpha}{32}\right) \tag{23}
$$
$$
x_5^2 = 2b^2 - 2b^2\ \cos\left(\frac{\alpha}{32}\right) \tag{24}
$$
Substituindo $(22)$ em $(24)$:
$$x_5^2 = 2b^2 - 2b^2 \cdot \left( \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}}\right) \tag{25}
$$
$$
x_5^2 = b^2 \left( 2-2\cdot\left( \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}}\right)\right) \tag{26}
$$
Extraindo a raiz em ambos os membros da igualdade, obtemos:
$$x_5 = \sqrt{ b^2 \left( 2-2\cdot\left( \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}}\right)\right)} \tag{27}
$$
$$
x_5 = b \cdot \sqrt{ 2-2\cdot \sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}}} \tag{28}
$$
O número $2$ a direita do sinal de menos pode adentrar ao radical a sua direita como $4$, já que é uma raiz quadrada. Obtendo:
$$x_5 = b \cdot \sqrt{ 2-\sqrt{\frac{\displaystyle 4+4\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}{2}}} \tag{29}
$$
$$
x_5 = b \cdot \sqrt{ 2-\sqrt{\displaystyle 2+2\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\sqrt{\frac{\displaystyle 1+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{4bc}}}{2}}}{2}}}{2}}}} \tag{30}
$$
Vamos repetir esse processo até alcançar o último radical:
$$x_5 = b \cdot \sqrt{ 2-\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\displaystyle \sqrt{\frac{4(a+b+c)(b+c-a)}{4bc}}}}}}} \tag{31}
$$
$$
x_5 = b \cdot \sqrt{ 2-\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}} \tag{32}
$$
Como $x_5 \approx \widehat{CQ}$, logo, o produto do raio $b$ por $\pi$ está para $180^\circ$, assim como o comprimento $x_5$ está para $\displaystyle \frac{\alpha}{32}$:
$$\frac{\pi b}{180^\circ} = \frac{\widehat{CQ}}{\displaystyle \frac{\alpha}{32}} \approx \frac{x_5}{\displaystyle \frac{\alpha}{32}} \tag{33}
$$
$$
\frac{ \alpha}{32} \approx \frac{180^\circ}{\pi b} \cdot x_5 \tag{34}
$$
$$
\alpha \approx \frac{180^\circ \cdot 32}{\pi b} \cdot x_5 \tag{35}
$$
Como conhecemos $x_5$, dado em $(32)$, basta substituí-lo em $(35)$:
$$\alpha \approx \frac{180^\circ\cdot 32 \cdot b \cdot \sqrt{ 2-\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}}}{\pi b} \tag{36}
$$
$$
\alpha \approx \frac{180^\circ\cdot 2^5}{\pi} \cdot \sqrt{ 2-\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\displaystyle \sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}} \tag{37}
$$
Exemplo 1:
O triângulo $\triangle ABC$ abaixo foi criado utilizando o software Geogebra, cujos lados medem: $b=5$, $a=3,859578650443242$ e $c=3,296562835249749$, o ângulo formado entre os lados $b$ e $c$ é igual a $\alpha = 50,49490712462559^\circ$.
[Figura 9: ângulos de um triângulo]
Aplicando a fórmula dada em $(37)$, obtemos um valor com precisão de $2$ casas decimais:
$$\alpha \approx \frac{180^\circ\cdot 2^5}{\pi} \cdot \sqrt{ 2-\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\sqrt{\displaystyle 2+\displaystyle \sqrt{3,27229361103}}}}}} \tag{38}
$$
$$
\alpha \approx 50,49331131106^\circ \tag{39}
$$
Exemplo 2:
O triângulo $\triangle ABC$ abaixo, possui lados medindo $a=3,051370289408014$, $b=3,517153011832249$ e $c=6,568523301240263$. O ângulo formado entre os lados $a$ e $b$ é igual a $179,99999998007129^\circ$.
[Figura 10: Ângulos de um triângulo]
Aplicando a fórmula dos radicais aninhados para obter o ângulo $\gamma$, temos como resultado $179,92772156694144^\circ$. Quando o ângulo tende a $180^\circ$, a fórmula com apenas $5$ iterações retorna um valor com precisão de uma casa decimal. Sendo assim, quanto maior o expoente de $2$ e o número de radicais à direita do sinal de menos, podemos obter ângulos cada vez mais precisos. No triângulo acima, aplicando a fórmula para $7$ iterações, obtemos $\gamma=179,9954820876601^\circ$ e para $10$ iterações, obtemos $\gamma=179,99992940672044^\circ$.
Generalização da fórmula
Note que a quantidade de radicais aninhados a direita do sinal de menos é exatamente o número de iterações que efetuamos.
[Figura 11: ângulo de um triângulo]
A cada iteração, fatiamos o ângulo $\alpha$ em $2$ elevado ao número de iterações que efetuamos.
[Figura 12: Iterações]
Generalizando para uma quantidade $n$ de iterações:
[Figura 13: O ângulo $\alpha$]
Analogamente, podemos repetir o procedimento acima para encontrarmos os ângulos $\beta$ e o ângulo $\gamma$.
[Figura 14: O ângulo $\beta$]
[Figura 15: O ângulo $\gamma$]
O radicando mais interno é a razão entre o produto do perímetro pela soma dos lados adjacentes ao ângulo menos o lado oposto ao ângulo, e o produto dos lados adjacentes ao ângulo.
[Figura 16: Ângulos de um triângulo]
O autor
- Este artigo foi elaborado por Rodrigo da Costa Moreira, licenciado em Matemática pelo Instituto Federal do Piauí - IFPI - Campus Uruçuí.
- Contato: https://twitter.com/rodrigo_cstm
Links para este artigo:
- https://bit.ly/formula-radicais-aninhados
- https://www.obaricentrodamente.com/2023/06/formula-para-calcular-as-medidas-dos-angulos-internos-de-um-triangulo-qualquer-em-funcao-de-seus-lados.html
